Grass on Grass

みどりの日なのでGrass書きました。今回はGrass言語インタプリタ上で動くGrass言語インタプリタ。

https://github.com/youz/Grass_on_Grass

Grassで実装されたGrassインタプリタ

この8kbとちょっとの草原を手で植えるのはさすがに厳しいので Grasspiler を使用して生成しています。

GrasspilerはSML風の文法で書いたラムダ式をGrassのコードにコンパイルしてくれる超便利ツール。 元コードはこんな感じ

https://github.com/youz/Grass_on_Grass/blob/master/grass.ml

実装方針

• データ構造はチャーチ対で表現
• App(m, n)のm, nとかの数値はチャーチ数
• オブジェクト識別用タグとしてGrassの基本型のCharを使用

データ構造が実質Consセル、つまりLispでGrassを書くみたいなもんですね。loopもcallccもありませんがまあそこは気合と根性とCPS変換と末尾再帰でなんとか。いやしかしパーサもうちょっとなんとかならんかな…

Grass on Grassを動かすGrass実装

ベースの処理系はスクリプト言語での実装とかでもHello world動かすくらいなら大丈夫そうですが、最終的にこの2kbほどあるQuineのコードをgrass.grass上で動かしたかったので、ある程度高速な実装を2つ用意しました。

C言語実装

https://github.com/youz/grasses/tree/master/C

要libgc。mingw64とdebianで動作確認してます。なおパーサが手抜きのため全角のｗＷｖを読めません。

F#実装

https://github.com/youz/grasses/tree/master/FSharp

こちらは全角ソース(UTF-8)も対応。処理速度はC実装よりほんのちょっと遅いくらいです。

(追記) Linux/WSL/MacOS環境ではmlgrass (OCaml実装) の ちょっと修正した奴をocamloptでコンパイルして使うと良いでしょう。 私のC実装の2～3倍速いです。

動かしてみる

以下C言語製インタプリタ上で動作確認

$ time grass grass.grass < examples/hello.grass
Hello, world!
real    0m0.060s
user    0m0.047s
sys     0m0.031s

Hello worldは難無く実行できますね。

$ time grass grass.grass < examples/quine.grass
wWwWwWwwWwwWwWwwWwWwWwWwWwWwWwWwwWwWwWwWwwWwWwWwWwwwWwWwWwwWwwWwWwwWwwWwwWwWwwwWwWwwWwwWwWwWwwWwWwWwWwwWwWwWwWwWwWwWwWwWwwWwWwWwWwWwwWwwWwWwwwWwWwwWwwWwwWwwWwWwwWwwWwwWwwWwWwWwWwWwwWwWwwWwWwWwWwwWwWwWwWwWwWwWwWwWwWwWwWwWwwwWwwWwWwWwwwWwWwwwWwwWwWwWwWwWwWwWwWwWwWwwWwwWwwWwwWwWwwWwwWwWwwwWwWwWwwWwwWwWwwWwWwWwWwWwwWwwWwwWwwWwwWwwWwwWwWwWwWwwWwwWwwWwwWwwWwWwwWwWwWwWwWwWwWwWwWwWwWwWwwWwWwWwWwWwWwWwWwWwWwwWwwWwwWwwWwwWwWwwwWwwWwwWwwWwwWwwWwWwWwWwWwWwWwWwWwWwWwWwWwwwWwWwwWwwWwWwwWwwWwwWwWwwwWwWwwWwwWwwWwWwWwWwWwWwWwWwWwWwwWwWwWwwWwWwWwWwWwWwwWwWwWwWwWwWwwWwwWwwWwwWwwWwwWwwWwWwWwWwWwWwWwWwWwWwwWwWwWwWwWwWwWwwWwWwwWwWwWwWwWwwWwWwWwWwWwwwWwWwWwwwWwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwWwwWwWwWwWwwWwwWwwWwwWwWwwWwWwWwWwWwWwWwWwWwwWwWwWwWwWwWwWwWwWwWwWwWwwWwWwwWwwWwwWwwWwwWwWwwWwWwWwWwWwWwWwWwWwWwWwwWwwWwwWwwWwwWwWwWwWwWwWwWwWwWwWwWwWwWwWwWwWwWwwWwwWwwWwWwWwWwWwWwWwwwWwWwWwWwwWwWwWwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwWwWwWwwWwwWwWwwwWwWwWwWwwWwwWwWwwWwwWwWwWwWwWwwwWwWwWwwwWwWwWwWwwWwWwWwWwWwwWwWwwWwwWwwWwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwWwWwWwwWwWwWwWwWwWwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwWwwWwWwWwWwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwWwwWwWwWwWwWwWwWwWwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwWwwwWwWwWwWwwWwwWwwWwWwWwWwwWwwWwWwWwWwWwWwWwwWwWwWwWwWwWwWwWwwWwwWwwWwwWwwWwwWwwWwWwWwWwwWwWwWwwWwwWwwWwWwWwWwwWwWwwWwWwWwWwWwWwWwWwWwWwWwWwWwwWwWwWwWwWwwWwWwWwWwwWwWwWwWwWwWwWwWwWwWwWwWwWwwwWwwWwWwwWwwWwwWwwWwwWwwWwWwWwWwWwwWwWwWwWwWwWwWwWwWwWwWwWwWwWwWwwWwwWwwWwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwvwwWWwWwwwwwwwWwwwWwwwvwwWWwWWWwvwWWwwWwwwWwwwwwwwwWwwwwWWwvwWWWWwWWWWwwwwWwWwwwWwwwwwwwwwwwwvWwwvwvWwwwwwwwwwWWWWwWWwvwwWWwWwwwwWWWWWWWwwwWWWWWwWwwwwwwwwwwwWwwwwwwwwwWWWWWwvWWWWWwwwwwwwwwwwwvwWWwWWWwvwWWWwwwwwwwwwWwwWwwwwwWwwwwwWWWWWWWwwwwwwwwwWwwwwwwWwWwwwwWwwwwvwwvwWWWWWWWWWWWWWWWWwWwwwWWWWwWwwwwwwwwWwwwwwwwwwwwWwWWWWWwWwwwwwwwwwwWWWWWwwwwwwwwwwwwwwwwWWWwwwwwwvwwwWwwwWWWWWWWWWWWWWwwwWWwvwwwWWwWWwwwwvwwvwwwWwwwwWwWWWwWWWWWWWWWWWWWWWwwwWwwwwwwWWWWWWWWWWwWwwwwWWWWWWWWWWWWWwWwwwwwwwwWWWWWWWWWWWWwvwwwWWWwwwWWwwwwwwWwwwwwwwWWWWWWWwwwWwwWWWwwwWwWwwwwwwwwwwwwWwwwwWwwwWwwwwwwwwwwwwvWwWWWWWWwwwwWwwwwwwwwwwwwwwWWWwWWWWWWWWWWw
real    0m1.475s
user    0m1.766s
sys     0m0.328s

Quineも無事ちゃんと動きました。

ちょっと困ったのが標準入力を扱うプログラムを動かしたい場合。 grassには文字列リテラルやファイル入出力機能が存在しないため、grass製インタプリタに与えるプログラムソースは標準入力から読ませるしかありません。 なのでこのGrass on Grassでは言語仕様を以下のようにちょっと変えています。

• 標準入力からの入力は、大文字のVまたはEOFまでをgrassプログラムソースとする
• Vを見つけてソースの読み込みを終えた場合、残りの入力をgrass.grassインタプリタ上で実行するプログラムへの入力とする

この仕様を利用したechoプログラムを実行してみます。

$ cat examples/echo.grass
wwwvwwWWwwWWWWWWWWwwwwWwWwwwwwwwWwwwWwwwwWWWWwwwwwwWwwWwwwvwWWwwWwVasdfqwer
$ grass grass.grass < examples/echo.grass
asdfqwer

上手く動いてますね。なお本家仕様通りのgrassインタプリタではV以降も普通にソースコードとして読み込みますので、Vの後ろにwWvがある場合動作が変わってしまうのでご注意。

さて、この入力の仕様を利用してこんな事が出来ちゃいます。

$ cat examples/grass2w.grass
wvWWWWwwwwvwWwwvwwvwWwwvwwwWwwwWwwwvWWWWWWWWwwwwwwwwwvwWWWWWWwWwwwwwwwwwwwwvwwWWWWWwwwwwwwwwwwwwWWWWWWwwwWwwwWWWwvwWWWWWWwWWWWWWWWWwvwWWWWWWWwWWWWWWWWwvwwwWWWwwWwwWWWWwvwWWWWWWWWWwWWWWWWWWWWWWwvwWWWWWWWWWWwWWWWWWWWWWWwvwwWWWWwwWWWWWWwWWWWWWWWWWWWWwwwWWWWWWwwwwwWWwWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWwwwwwWwwwWWWwvWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWwvwWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwwWwwvwWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWwWWWWwvwWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWwWWWWWwvwwwvwWWWWWWWWWWWWWWWWWWWWWWWWWWwwWwWWWWWWWwwWWwWwwwwwvwWWWWWWWWWWWWWWWWWWwwwwwwwwWwwvwWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWwwwwwwwWWWWwwwwwwwWWWWWwwwwwwWWWWWWWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWWWWWWwwwwWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWwWWWWWwWWWWWWWwvwwWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWwwwWwwwWWWwvwWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWwvwWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWwvwwWWwvwwWWwWWWwvwwvWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWwwWwwwWWWwvwWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwWwwwwwwwwwwWWWwWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwWwwWWWWWWWWWWWWWWWWWwwwwwwwWwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWwwwWwwvWwwvwWWWWWWWWWWWWWWWWWWWWWWWwWwwWWWWWWWWWWWWWWWwWwwwwwwwwwwwvWwwwwvwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWwWwwwwwwwwWwwwwwwwvwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWwwvwwwWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwWwwwwwwwWWWwWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwvwwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwvwwwWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwWWWWWwWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWwwwwwwwwwwWwwwwwwWWWwWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWwwwwwwwwwWWwWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwWWwWWWWWWwWwwwwwwwwwwwvwwWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWwwwwwWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwWwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwWwwwwwwwwwwwwWWWwvwwvwWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwWWWWWWWwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwWwwWwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwWwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwWWwWWWWWWWWWWWwvwwWWwWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwvwwWWwWWWwvwwWWWwwwwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWwWWWWWWwwwwWwwWWwWwwwwwwwwvwvWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWwWwwwwwwWWwwwwwwWWWWWWwWwwwwwwwwwWwvwwvwwWWwwwwWwwvwWwwwwwwwwwwWWWwWWWwwwwwwwwwWWWWWwWWWWWwwwwwwwwwwwwWWwWWWWWwvwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwWwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwWWWWWWwvwwwwwWWWWWwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwWWWWWWWWWWWWWwWWWWWWWWWwwwwwwwWwwwwwwwWwwwwwwwWWWWwWWWWWWWWWWWwwwwwwWWWWWWWWwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwWWwWwwwwwwwwwwwwwWWWWWwWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwWWWWWWWWWWWWWWwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwWWWWwWWWWWWWwWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwwwwwwWWWWwWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwvwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwWwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwwwwwwWWWWWWwwwwwwWwwwwwwwwwwwwwwwwWwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwwWwwwwwvwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwvwwwwwvwWwwWwwwwwwwwwwwvwwWWwwWWWWwwWwwwwwwwWwWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwWWwWwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwWWwvWwvwvWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwvwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWwwwWWwWwwwwwwwwwwwwwwwwwWwWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwWWwvwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwWWWWwvwwwwwWWWWWwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWwWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwWWwWwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwWwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwWWWWWWWWwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWwwWwwwwWWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwwwwvwWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWwWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwWWwWwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwwwwvwwwwWWWWwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwWWWWwWwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWwwwwWWWWwwwwwwwwwwwwwwwwwwwwWwwwwwwwWWWwWWWWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwvwWWWWWWWWWwWWWwwwWwwWwwwwwwwwwwwWwvwWWWWWWWWWWWWWWWwWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWw
VwWWwwww
$ time grass grass.grass < examples/grass2w.grass
w
real    0m0.387s
user    0m0.328s
sys     0m0.016s

grass2w.grassの1行目はgrassインタプリタで、V以降はwを1個出力するプログラム。 つまりC製grassインタプリタの上でgrass製grassインタプリタを動作させ、そこにまたgrass製grassインタプリタを読み込ませて動かした上でwを1文字表示するプログラムを実行しています。

もうちょっと重いやつを

$ time grass grass.grass < examples/grass2hello.grass
Hello, world!
real    0m2.491s
user    0m2.859s
sys     0m0.188s

Hello world on grass.grass on grass.grass on grass.c。まだ余裕ありそうですね。

$ time grass grass.grass < examples/grass2quine.grass
wWwWwWwwWwwWwWwwWwWwWwWwWwWwWwWwwWwWwWwWwwWwWwWwWwwwWwWwWwwWwwWwWwwWwwWwwWwWwwwWwWwwWwwWwWwWwwWwWwWwWwwWwWwWwWwWwWwWwWwWwwWwWwWwWwWwwWwwWwWwwwWwWwwWwwWwwWwwWwWwwWwwWwwWwwWwWwWwWwWwwWwWwwWwWwWwWwwWwWwWwWwWwWwWwWwWwWwWwWwWwwwWwwWwWwWwwwWwWwwwWwwWwWwWwWwWwWwWwWwWwWwwWwwWwwWwwWwWwwWwwWwWwwwWwWwWwwWwwWwWwwWwWwWwWwWwwWwwWwwWwwWwwWwwWwwWwWwWwWwwWwwWwwWwwWwwWwWwwWwWwWwWwWwWwWwWwWwWwWwWwwWwWwWwWwWwWwWwWwWwWwwWwwWwwWwwWwwWwWwwwWwwWwwWwwWwwWwwWwWwWwWwWwWwWwWwWwWwWwWwWwwwWwWwwWwwWwWwwWwwWwwWwWwwwWwWwwWwwWwwWwWwWwWwWwWwWwWwWwWwwWwWwWwwWwWwWwWwWwWwwWwWwWwWwWwWwwWwwWwwWwwWwwWwwWwwWwWwWwWwWwWwWwWwWwWwwWwWwWwWwWwWwWwwWwWwwWwWwWwWwWwwWwWwWwWwWwwwWwWwWwwwWwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwWwwWwWwWwWwwWwwWwwWwwWwWwwWwWwWwWwWwWwWwWwWwwWwWwWwWwWwWwWwWwWwWwWwWwwWwWwwWwwWwwWwwWwwWwWwwWwWwWwWwWwWwWwWwWwWwWwwWwwWwwWwwWwwWwWwWwWwWwWwWwWwWwWwWwWwWwWwWwWwWwwWwwWwwWwWwWwWwWwWwWwwwWwWwWwWwwWwWwWwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwWwWwWwwWwwWwWwwwWwWwWwWwwWwwWwWwwWwwWwWwWwWwWwwwWwWwWwwwWwWwWwWwwWwWwWwWwWwwWwWwwWwwWwwWwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwWwWwWwwWwWwWwWwWwWwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwWwwWwWwWwWwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwWwwWwWwWwWwWwWwWwWwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwWwwwWwWwWwWwwWwwWwwWwWwWwWwwWwwWwWwWwWwWwWwWwwWwWwWwWwWwWwWwWwwWwwWwwWwwWwwWwwWwwWwWwWwWwwWwWwWwwWwwWwwWwWwWwWwwWwWwwWwWwWwWwWwWwWwWwWwWwWwWwWwwWwWwWwWwWwwWwWwWwWwwWwWwWwWwWwWwWwWwWwWwWwWwWwwwWwwWwWwwWwwWwwWwwWwwWwwWwWwWwWwWwwWwWwWwWwWwWwWwWwWwWwWwWwWwWwWwwWwwWwwWwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwwWwvwwWWwWwwwwwwwWwwwWwwwvwwWWwWWWwvwWWwwWwwwWwwwwwwwwWwwwwWWwvwWWWWwWWWWwwwwWwWwwwWwwwwwwwwwwwwvWwwvwvWwwwwwwwwwWWWWwWWwvwwWWwWwwwwWWWWWWWwwwWWWWWwWwwwwwwwwwwwWwwwwwwwwwWWWWWwvWWWWWwwwwwwwwwwwwvwWWwWWWwvwWWWwwwwwwwwwWwwWwwwwwWwwwwwWWWWWWWwwwwwwwwwWwwwwwwWwWwwwwWwwwwvwwvwWWWWWWWWWWWWWWWWwWwwwWWWWwWwwwwwwwwWwwwwwwwwwwwWwWWWWWwWwwwwwwwwwwWWWWWwwwwwwwwwwwwwwwwWWWwwwwwwvwwwWwwwWWWWWWWWWWWWWwwwWWwvwwwWWwWWwwwwvwwvwwwWwwwwWwWWWwWWWWWWWWWWWWWWWwwwWwwwwwwWWWWWWWWWWwWwwwwWWWWWWWWWWWWWwWwwwwwwwwWWWWWWWWWWWWwvwwwWWWwwwWWwwwwwwWwwwwwwwWWWWWWWwwwWwwWWWwwwWwWwwwwwwwwwwwwWwwwwWwwwWwwwwwwwwwwwwvWwWWWWWWwwwwWwwwwwwwwwwwwwwWWWwWWWWWWWWWWw
real    3m5.496s
user    3m47.625s
sys     0m1.422s

Quine on grass.grass on grass.grass on grass.c。3分かかりましたが完遂しました。

ではもう一段

$ cat examples/grass3w.grass
wvWWWWwwwwvwWwwvwwvwWwwvwwwWwwwWwwwvWWWWWWWWwwwwwwwwwvwWWWWWWwWwwwwwwwwwwwwvwwWWWWWwwwwwwwwwwwwwWWWWWWwwwWwwwWWWwvwWWWWWWwWWWWWWWWWwvwWWWWWWWwWWWWWWWWwvwwwWWWwwWwwWWWWwvwWWWWWWWWWwWWWWWWWWWWWWwvwWWWWWWWWWWwWWWWWWWWWWWwvwwWWWWwwWWWWWWwWWWWWWWWWWWWWwwwWWWWWWwwwwwWWwWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWwwwwwWwwwWWWwvWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWwvwWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwwWwwvwWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWwWWWWwvwWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWwWWWWWwvwwwvwWWWWWWWWWWWWWWWWWWWWWWWWWWwwWwWWWWWWWwwWWwWwwwwwvwWWWWWWWWWWWWWWWWWWwwwwwwwwWwwvwWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWwwwwwwwWWWWwwwwwwwWWWWWwwwwwwWWWWWWWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWWWWWWwwwwWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWwWWWWWwWWWWWWWwvwwWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWwwwWwwwWWWwvwWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWwvwWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWwvwwWWwvwwWWwWWWwvwwvWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWwwWwwwWWWwvwWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwWwwwwwwwwwwWWWwWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwWwwWWWWWWWWWWWWWWWWWwwwwwwwWwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWwwwWwwvWwwvwWWWWWWWWWWWWWWWWWWWWWWWwWwwWWWWWWWWWWWWWWWwWwwwwwwwwwwwvWwwwwvwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWwWwwwwwwwwWwwwwwwwvwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWwwvwwwWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwWwwwwwwwWWWwWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwvwwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwvwwwWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwWWWWWwWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWwwwwwwwwwwWwwwwwwWWWwWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWwwwwwwwwwWWwWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwWWwWWWWWWwWwwwwwwwwwwwvwwWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWwwwwwWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwWwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwWwwwwwwwwwwwwWWWwvwwvwWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwWWWWWWWwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwWwwWwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwWwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwWWwWWWWWWWWWWWwvwwWWwWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwvwwWWwWWWwvwwWWWwwwwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWwWWWWWWwwwwWwwWWwWwwwwwwwwvwvWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWwWwwwwwwWWwwwwwwWWWWWWwWwwwwwwwwwWwvwwvwwWWwwwwWwwvwWwwwwwwwwwwWWWwWWWwwwwwwwwwWWWWWwWWWWWwwwwwwwwwwwwWWwWWWWWwvwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwWwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwWWWWWWwvwwwwwWWWWWwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwWWWWWWWWWWWWWwWWWWWWWWWwwwwwwwWwwwwwwwWwwwwwwwWWWWwWWWWWWWWWWWwwwwwwWWWWWWWWwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwWWwWwwwwwwwwwwwwwWWWWWwWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwWWWWWWWWWWWWWWwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwWWWWwWWWWWWWwWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwwwwwwWWWWwWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwvwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwWwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwwwwwwWWWWWWwwwwwwWwwwwwwwwwwwwwwwwWwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwwWwwwwwvwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwvwwwwwvwWwwWwwwwwwwwwwwvwwWWwwWWWWwwWwwwwwwwWwWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwWWwWwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwWWwvWwvwvWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwvwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWwwwWWwWwwwwwwwwwwwwwwwwwWwWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwWWwvwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwWWWWwvwwwwwWWWWWwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWwWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwWWwWwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwWwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwWWWWWWWWwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWwwWwwwwWWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwwwwvwWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWwWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwWWwWwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwwwwvwwwwWWWWwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwWWWWwWwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWwwwwWWWWwwwwwwwwwwwwwwwwwwwwWwwwwwwwWWWwWWWWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwvwWWWWWWWWWwWWWwwwWwwWwwwwwwwwwwwWwvwWWWWWWWWWWWWWWWwWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWw
VwvWWWWwwwwvwWwwvwwvwWwwvwwwWwwwWwwwvWWWWWWWWwwwwwwwwwvwWWWWWWwWwwwwwwwwwwwwvwwWWWWWwwwwwwwwwwwwwWWWWWWwwwWwwwWWWwvwWWWWWWwWWWWWWWWWwvwWWWWWWWwWWWWWWWWwvwwwWWWwwWwwWWWWwvwWWWWWWWWWwWWWWWWWWWWWWwvwWWWWWWWWWWwWWWWWWWWWWWwvwwWWWWwwWWWWWWwWWWWWWWWWWWWWwwwWWWWWWwwwwwWWwWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWwwwwwWwwwWWWwvWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWwvwWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwwWwwvwWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWwWWWWwvwWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWwWWWWWwvwwwvwWWWWWWWWWWWWWWWWWWWWWWWWWWwwWwWWWWWWWwwWWwWwwwwwvwWWWWWWWWWWWWWWWWWWwwwwwwwwWwwvwWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWwwwwwwwWWWWwwwwwwwWWWWWwwwwwwWWWWWWWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWWWWWWwwwwWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWwWWWWWwWWWWWWWwvwwWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWwwwWwwwWWWwvwWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWwvwWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWwvwwWWwvwwWWwWWWwvwwvWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWwwWwwwWWWwvwWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwWwwwwwwwwwwWWWwWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwWwwWWWWWWWWWWWWWWWWWwwwwwwwWwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWwwwWwwvWwwvwWWWWWWWWWWWWWWWWWWWWWWWwWwwWWWWWWWWWWWWWWWwWwwwwwwwwwwwvWwwwwvwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWwWwwwwwwwwWwwwwwwwvwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWwwvwwwWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwWwwwwwwwWWWwWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwvwwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwvwwwWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwWWWWWwWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWwwwwwwwwwwWwwwwwwWWWwWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWwwwwwwwwwWWwWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwWWwWWWWWWwWwwwwwwwwwwwvwwWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWwwwwwWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwWwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwWwwwwwwwwwwwwWWWwvwwvwWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwWWWWWWWwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwWwwWwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwWwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwWWwWWWWWWWWWWWwvwwWWwWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwvwwWWwWWWwvwwWWWwwwwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWwWWWWWWwwwwWwwWWwWwwwwwwwwvwvWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWwWwwwwwwWWwwwwwwWWWWWWwWwwwwwwwwwWwvwwvwwWWwwwwWwwvwWwwwwwwwwwwWWWwWWWwwwwwwwwwWWWWWwWWWWWwwwwwwwwwwwwWWwWWWWWwvwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwWwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwWWWWWWwvwwwwwWWWWWwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwWWWWWWWWWWWWWwWWWWWWWWWwwwwwwwWwwwwwwwWwwwwwwwWWWWwWWWWWWWWWWWwwwwwwWWWWWWWWwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwWWwWwwwwwwwwwwwwwWWWWWwWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwWWWWWWWWWWWWWWwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwWWWWwWWWWWWWwWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwwwwwwWWWWwWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwvwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwWwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwwwwwwWWWWWWwwwwwwWwwwwwwwwwwwwwwwwWwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwwWwwwwwvwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwvwwwwwvwWwwWwwwwwwwwwwwvwwWWwwWWWWwwWwwwwwwwWwWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwWWwWwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwWWwvWwvwvWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwvwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWwwwWWwWwwwwwwwwwwwwwwwwwWwWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwWWwvwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwWWWWwvwwwwwWWWWWwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWwWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwWWwWwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwWwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwWWWWWWWWwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWwwWwwwwWWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwwwwwwvwWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWwWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwwwwwwwwwwwwWWwWwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwwwwvwwwwWWWWwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwWWWWwWwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwWWWWWWWWWWWWWWWWWWwWwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWwwwwWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwWwwwwwwwwwwwwwwwwwwWWWWWWWWWWWWWWWWWwwwwWWWWwwwwwwwwwwwwwwwwwwwwWwwwwwwwWWWwWWWWWwWwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwvwWWWWWWWWWwWWWwwwWwwWwwwwwwwwwwwWwvwWWWWWWWWWWWWWWWwWWWwWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWw
VwWWwwww

$ time grass grass.grass < examples/grass3w.grass
w
real    0m31.284s
user    0m31.516s
sys     0m0.422s

grass.grass3段重ね on grass.c。まだ動いてる

$ time grass grass.grass < examples/grass3hello.grass
Hello, world!
real    8m3.880s
user    8m54.188s
sys     0m1.938s

Hello world on grass.grass3段重ね on grass.c は8分かかってなんとか完遂。Quine on 3段重ねは流石に暑くなってきたので止めました。

最初は2段重ねが出来たらいいなーくらいの気持ちだったので3段行けたのは嬉しいですね。

余談

grassのCharの適用規則なんですけど、公式の説明とSML実装を読む限りではOutやらSuccやらのCharでない物を引数として渡すとチャーチboolのfalseが返ってくるようになってるっぽいんですが、

  fun charEq (CH c1, CH c2) = if c1 = c2 then churchTrue else churchFalse
    | charEq _ = churchFalse

公式のruby(1.8)実装やgolf場で採用されてるOCaml実装ではChar以外を渡すとエラーになっちゃうんですよね。 エラー終了するのではなくfalseを返してくれる方が色々と便利なので、うちのリポジトリに置いてある実装はどれもfalseを返すようにしてあります。

SATySFiでテントを描くコマンド作った

これは2018 SATySFi advent calendar 20日目の記事です。[前] [次]

現在の文脈のフォントサイズに合わせてテントを建てるコマンドを作りました。

このGistに入っているsatyhファイル

• affinetransform.satyh
• flexpath.satyh
• camp.satyh

上記3つをコピーしてきて@import: campすると\Tentコマンドが使えるようになります。

引数はfloat * float型のタプルで、(0.0, 0.0)がニュートラル、数値を増やしたり減らしたりするとクネクネします。

使用例

@require: stdja
@import: camp

let-inline ctx \fsz sz it =
  let c = set-font-size sz ctx in
    read-inline c it

in
document (|
  title = {\Tent((0.0, 0.0));};
  author = {};
  show-title = true;
  show-toc = false;
|) '<
  +p{
    \fsz(40pt){
      \Tent((0.0, 0.0));
      \Tent((0.2, 0.1));
      \Tent((0.4, 0.2));
      \Tent((0.1, 0.1));
      \Tent((0.0, 0.0));
      \Tent((0.2, 0.1));
      \Tent((0.4, 0.2));
      \Tent((0.1, 0.1));
      \Tent((0.0, 0.0));
    }
  }
>

出力結果↓

enjoy!

ゆるキャン△テントマーク高耐久ステッカー

www.amazon.co.jp

SATySFiでお絵描き

これは2018 SATySFi advent calendar 16日目の記事です。[前] [次]

SATySFiには基本的な図形描画機能が備わっていますが、「え…ベクタ描画? そんなハイカラなの難しそう…ドットで描けないの…?」みたいな人もいると思うので、疑似ピクセル単位で画像を描画するコマンドを作ってみました。

https://github.com/youz/satysfi-pixels

使い方

上記リポジトリからpixels.satyhを持ってきて、packagesディレクトリに放り込んで@require: pixelsするか、書いてる文書と同じフォルダに置いて@import: pixelsして下さい。 するとインラインコマンド\Pixelsが使えるようになります。

% Pixelsコマンドのシグネチャ
   \Pixels : [length * length * length; int * int; int -> int -> color] inline-cmd

• 第1引数は出力する画像の幅, 高さ, 深さのタプル (最終的にinline-graphics関数に渡す値)
• 第2引数は画像のピクセル数での幅, 高さのタプル
• 第3引数はx, y座標を受け取ってcolorを返す関数

となっています。

使用例1

@require: stdja
@import: pixels

let get-color x y =
  Gray(float x /. 255.)

in
document (|
  title = {gradation sample 1};
  author = {};
  show-title = false;
  show-toc = false;
|) '<
  +p{
    \Pixels((100pt, 100pt, 0pt))((256, 256))(get-color);
  }
>

get-color関数は受け取ったx座標を255で割り、モノクロ色の値として返します。

本文中の\Pixelsコマンドの引数は、「出力サイズが100pt x 100ptで画素数が256px×256pxのgraphicsを生成して埋め込みます。各ピクセルのRGB値はget-color関数で決定します。」という意味になります。

これをコンパイルすると下図のような画像がインライングラフィクスとして出力されます。

サンプル1

もう1つサンプルコード

@require: stdja
@import: pixels

let get-color x y =
  let r = x mod 256 in
  let g = y mod 256 in
  let b = 255 - (x mod 256) in
    RGB(float r /. 255., float g /. 255., float b /. 255.)

in
document (|
  title = {gradation sample 2};
  author = {};
  show-title = false;
  show-toc = false;
|) '<
  +p{
    \Pixels((100pt, 100pt, 0pt))((512, 512))(get-color);
  }
>

今度はモノクロではなくカラーで。 RGB各色を以下のように座標から決定するようにしています。

• R = x mod 256 / 255
• G = y mod 256 / 255
• B = (255 - (x mod 256)) /255

また、画像サイズは変わりませんがピクセル数を512x512に変更しました。(解像度が変わります)

すると今度は下図のような出力になります。

サンプル2

その他、ソースリポジトリに入れてあるサンプルを画像だけ紹介

bitxor (x ^ y)

マンデルブロ集合

Ambient Occlusionによるレンダリング (こちらのコードを移植)

楽しいですね。いろいろ関数つっこんで遊んでみて下さい。

なおピクセル数を増やして行くとPDFビュアーでの描画が目に見えて重くなるのでそこはご注意を。

SATySFiで数式を生成する ～ラムダ計算編～

これは2018 SATySFi advent calendar 13日目の記事です。[前] [次]

たとえば何かの資料を書いてる中でラムダ計算の説明が必要になった時、ちょっと込み入ったサンプルを手で書こうとしたら大変です。

PRED 5
 = (λnfx.n (λgh.h(gf)) (λu.x) (λu.u)) (λfx.f(f(f(f(fx)))))
 → λfx.(λf'x'.f'(f'(f'(f'(f'x'))))) (λgh.h(gf)) (λu.x) (λu.u)
 → λfx.(λgh.h(gf)) ((λgh.h(gf)) ((λgh.h(gf)) ((λgh.h(gf)) ((λgh.h(gf)) (λu.x))))) (λu.u)
 → ▂▅▇█▓▒░(‘ω’)░▒▓█▇▅▂

心を無にして手を動かせばどうとでもなるんでしょうが誤植が怖い。

そこでSATySFiを使えば計算から組版まで全自動で出来ちゃうんじゃないかな? という事で、ラムダ計算の計算式の生成方法を考えて行きます。

1. データ表現と計算処理の実装

考えて行きますと言ったばかりですが、計算方法についてこれはもうとても素晴らしい講義資料を東北大の住井先生が公開して下さってますので、まずそちらをご覧ください。

ラムダ計算入門(pdf)

OCamlによるラムダ計算インタプリタのシンプルな実装が載っていて、ほぼそのままSATySFiに移植できちゃいます。 が、後の組版処理の都合でちょっと改変を加えます。

データ表現とgensym関数

β簡約時の変数名衝突を避けるために一意な名前の変数を生成するgensym関数ですが、資料のコードでは変数名が'g'+連番となっています。 まあg+添字で出力しても良いのですが、せっかくなのでアルファベット+0個以上のプライムで出力するようにしてみましょう、という事でまずラムダ式のデータ型expを以下のように改変。

type exp =
  | Var of string * int
  | Abs of exp * exp
  | App of exp * exp

Var(変数)はただのstringから(string * int)に変更。stringは変数名、intはプライムの数を表します。

それとAbs(λ抽象)のタプルの1要素目(パラメータ変数名)をstringからexp(実際はVarしか入らない)に変更しています。

gensym関数はカウンタを使う所は変わりませんが、カウンタ値を26で割った余りを文字種(a-z)、商をプライムの数とします。また、ユーザー入力の変数名と被らないようにする処理を加えます。

% 変数名比較関数
let vareq x y =
  match (x, y) with
  | (Var(s, i), Var(t, j)) -> string-same s t && i == j
  | _ -> false

% 汎用リスト検索関数
let-rec find eq x l =
  match l with
  | []     -> None
  | e :: r -> if eq x e then Some(e) else find eq x r

% gensym用カウンタ
let-mutable sym-counter <- -1

% ユーザー入力式中の全変数を入れておくリスト
let-mutable sym-used <- []

% 変数生成関数
let-rec gensym () =
  let () = sym-counter <- !sym-counter + 1 in
  let c = string-unexplode [!sym-counter mod 26 + 97] in
  let p = !sym-counter / 26 in
  let v = Var(c, p) in
    match find vareq v !sym-used with
    | None   -> v
    | Some _ -> gensym ()

sym-usedには計算開始前にユーザー入力の式の中の全変数が突っ込まれると思ってください。

計算処理

1ステップ分計算を進めるstep関数ですが、資料の実装ではβ簡約できる箇所が複数あった場合それぞれ計算して結果全部をlistにして返すようになっていて、それはそのままでも良いのですが今回は最終的に1通りの簡約方法でしか出力しないので1つの結果をoptionで返す(簡約できなかったらNoneを返す)ように変更します。

let-rec step e =
  match e with
  | Var(x) -> None
  | Abs(x, e0) -> (
    match step e0 with
    | None -> None
    | Some(e) -> Some(Abs(x, e))
    )
  | App(e1, e2) -> (
    match e1 with
    | Abs(x, e0) -> Some(subst e2 x e0)
    | _ -> (
      match step e1 with
      | Some(e) -> Some(App(e, e2))
      | None -> (
        match step e2 with
        | Some(e) -> Some(App(e1, e))
        | None -> None
      )))

簡約できなくなるまで計算を進めるrepeat関数は、途中経過の式をlistに溜め込むよう改変し、ついでにreduct-allと名前を変えます。また、簡約が停止しないタイプの式を与えられた時に死なないよう簡約回数のリミッタを指定できるようにしました。

let reduct-all e lim =
  let-rec r e a i =
    if i > lim then
      List.reverse (e :: a)
    else 
      match step e with
      | None -> List.reverse (e :: a)
      | Some(f) -> r f (e :: a) (i + 1)
  in
    r e [] 0

ここまでをざっくりテスト。 exp型データを文字列化する関数exp2strを用意し、(λf.λx.f(fx))(λf.λx.f(fx))を計算させてコンソールに出力してみます。

% 必要ない括弧が沢山付くけどキニシナイ
let-rec exp2str
  | (Var(x, i)) = x ^ (if i > 0 then (arabic i) else ` `)
  | (Abs(x, e)) = `(\` ^ (exp2str x) ^ `.` ^ (exp2str e) ^ `)`
  | (App(x, y)) = `(` ^ (exp2str x) ^ (exp2str y) ^ `)`

let-inline \test =
  let f = Var(`f`, 0) in
  let x = Var(`x`, 0) in
  let f2x = Abs(f, Abs(x, App(f, App(f, x)))) in
  let () = sym-used <- [f; x] in
  let () = reduct-all (App(f2x, f2x)) 100
         |> List.iter (fun e -> display-message (exp2str e))
  in
    {done}

コンソール出力結果

...
 ---- ---- ---- ----
  evaluating texts ...
((\f.(\x.(f(fx))))(\f.(\x.(f(fx)))))
(\a.((\f.(\x.(f(fx))))((\f.(\x.(f(fx))))a)))
(\a.(\b.(((\f.(\x.(f(fx))))a)(((\f.(\x.(f(fx))))a)b))))
(\a.(\b.((\c.(a(ac)))(((\f.(\x.(f(fx))))a)b))))
(\a.(\b.(a(a(((\f.(\x.(f(fx))))a)b)))))
(\a.(\b.(a(a((\d.(a(ad)))b)))))
(\a.(\b.(a(a(a(ab))))))
  evaluation done.
 ---- ---- ---- ----
...

良さそうな感じですね。

2. 数式化

さて本題。exp型データを数式化します。

まず変数Varの文字列化ですが、数式モードで書くようなx''と言った文字列を何も考えずにmath-charに渡すと

let-math \testvar = math-char MathOrd `x''`

...

  +p{${ \testvar }}

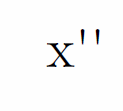
xは直立になるし、プライムを付けるつもりがシングルクォートになってしまっています。math-charは渡された文字列の数式構造を解析したりしないので、xを変数名として認識してイタリックにしたり、シングルクォートをプライムに置き換えたりみたいな事はしないんですね。

ではどうしたら良いかと言うと、文字列を渡すと斜体の数式にして返す\mathit-tokenというコマンドがありまして、変数名部分はコイツを使えばOK。

そしてプライムについては、シングルクォートを置き換えてくれないなら最初からプライム(U+2032)を書いちゃいます。

では実際にexp型のVarデータを数式化してみましょう。

let-rec repeat-string
  | s 0 = ` `
  | s n = s ^ (repeat-string s (n - 1))

let-math \testvar2 e =
  match e with
  | Var(s, n) ->
    let primes = math-char MathOrd (repeat-string `´` n) in
      math-concat ${\mathit-token!(s)} primes
  | _         -> ${}

...

  +p{${ \testvar2!(Var(`x`, 2)) }}

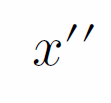
イイ感じになりましたね。そして変数の数式化が出来ちゃえば後はそんなに難しくありません。というわけでドーン

let-rec exp2math
  | (Var(x, i)) =
    let p = math-char MathOrd (repeat-string `′` i) in
      ${\mathit-token!(x)#p}
  | (Abs(x, e)) =
    let mx = exp2math x in
    let me = exp2math e in
      ${\lambda #mx . #me}
  | (App(x, y)) =
    let mx = exp2math x in
    let px = match x with
      | Var _         -> mx
      | App(_, Var _) -> mx
      | _ -> ${\(#mx\)}
    in
    let my = exp2math y in
    let py = match y with
      | Var _ -> my
      | _     -> ${\(#my\)}
    in
      math-concat px py

Absはアッカーマン関数の時のFunと同じ要領で、パラメータ(x)と式(e)をそれぞれ数式化しておいてリテラルへ埋め込んじゃえばOk。

Appは括弧が必要な場合と不要な場合の判定でちょっと長くなっちゃってますが、Absと同じようにxとyを再帰処理で数式化した上で、必要な箇所に括弧を貼り付けて横に並べるだけ。

試しに\f'.\x'.f'(f'x')を数式化してみましょう

let-math \testexpr = 
  let f = Var(`f`, 1) in
  let x = Var(`x`, 1) in
    exp2math (Abs(f, Abs(x, App(f, App(f, x)))))

...

  +p{ ${ \textexpr } }

結果

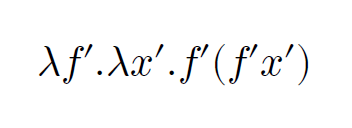
上手に出来ました。(実は問題が潜んでますがそこは追記で説明)

3. 数式を並べる

必要な機能がほぼ揃ったので、仕上げとしてブロックコマンド+lambdacalcを作成します。 gensymで使うカウンタと使用済み変数リストを初期化してから、渡された式を計算→数式化→縦に並べて完成。

今回はページをまたぐような長さの計算をするつもりはないので、数式を並べるのはmathパッケージの+alignコマンドに丸投げです。

let-block ctx +lambdacalc lm lexp =
  let () = sym-counter <- -1 in                         % gensym用カウンターリセット
  let () = sym-used <- (dedup vareq (allvar lexp)) in   % gensymでの名称被り回避用
  let (f::r) = reduct-all lexp 100
             |> List.map exp2math in
  let ml = [lm; ${= #f}] :: (List.map (fun m -> [${}; ${\to #m}]) r) in
    read-block ctx '<+align(ml);>

こんな風に使います。

...

% ラムダ式を簡単に書くためのエイリアス
let var s = Var(s, 0)
let abs v e = Abs(v, e)
let app e1 e2 = App(e1, e2)

% チャーチ数生成
let cnum n =
  let f = var `f` in
  let x = var `x` in
  let-rec r
    | 0 a = a
    | i a = r (i - 1) (app f a)
  in
    abs f (abs x (r n x))

in
document (| title = {}; author = {}; show-title = false; show-toc = false; |) '<
  +lambdacalc(${3^2})(app (cnum 2) (cnum 3));
>

チャーチ数の3の2乗

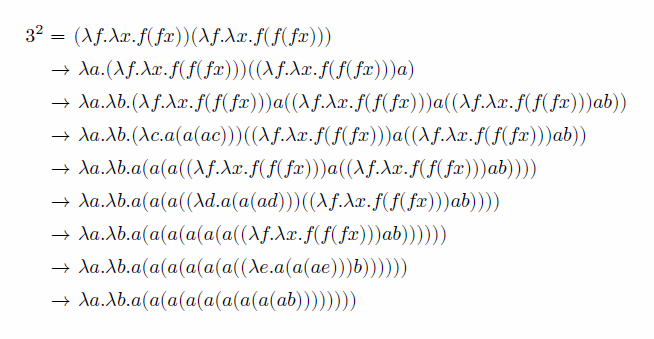
これでメンドクサイ引き算も安心

...
% pred = λn.λf.λx.n (λg.λh.h (g f)) (λu.x) (λu.u)
let pred =
  let f = var `f` in
  let g = var `g` in
  let h = var `h` in
  let n = var `n` in
  let u = var `u` in
  let x = var `x` in
    abs n (abs f (abs x (app (app (app n (abs g (abs h (app h (app g f))))) (abs u x)) (abs u u))))

in
document (| title = {}; author = {}; show-title = false; show-toc = false; |) '<
  +lambdacalc(${\text!({pred})\ 3})(app pred (cnum 3));
>

メンドクサイ引き算 (3 - 1)

以上ラムダ計算をSATySFiに自動で計算＆組版させる方法でした。

ソース全体はこちらのGistに。

色々計算させて遊んでみてください。

追記

実はプライムの付け方がこれでは不正解っぽいのです。 上がexp2mathで生成した数式、下が手打ちの数式\lambda f'. \lambda x'.f'\(f'x'\) をデバッグモードで出力した結果です。プライムは上付きにしないといけないんですね。

math-supという関数で上付きにできるようなので

let-rec exp2math
  | (Var(x, i)) =
    let p = math-char MathOrd (repeat-string `′` i) in
      math-sup ${\mathit-token!(x)} p
...

としてみましたが、そうすると

上がmath-supを使った生成式・下が手打ち

上下の位置は合いましたが、fとプライムの水平方向のスペースがなく、かえって見映えが悪くなる結果に。

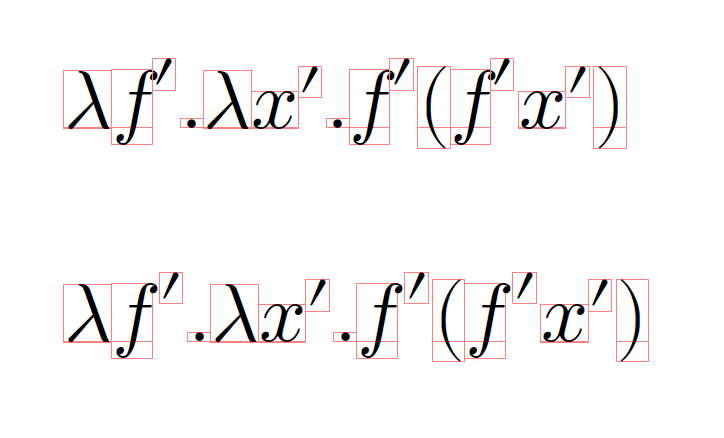
ちょっと調べてもこのスペースの正しい取り方が分からなかったので、これは今後の課題と言うことで。

SATySFiの可換図式パッケージの使い方

これは2018 SATySFi advent calendar 11日目の記事です。[前] [次]

SATySFiの標準パッケージの中に可換図式(comutative-diagram)を書くためのcdというパッケージがあるんですが、説明がThe SATySFi Bookや公式ドキュメントの中に見当たらなかったような気がするので使い方を紹介してみます。

1. モジュールインターフェース

cdパッケージのソースcd.satyhを開いてみると以下のようなシグネチャが書いてあります

module CD : sig
  type obj
  val \diagram : [length; length; (|
      obj             : point -> math -> obj;
      draw-obj        : obj -> graphics list;
      draw-arr        : math -> float?-> length ?-> obj -> obj -> graphics list;
      draw-dashed-arr : math -> float?-> length ?-> obj -> obj -> graphics list;
    |) -> graphics list] inline-cmd
end = struct

コマンドは\diagramというインラインコマンドが1つだけあります。 型を見ると、lengthを2つと”何かよくわからんレコードを受け取ってgrahicsのlistを返す関数”を引数に取るコマンドになっていて、この最後の関数はナニ??って話なんですが、これはLisp/Schemeによくあるcall-with-なんとか系の関数に渡す関数、あるいはRubyで言うとFile.openとかのメソッドに渡すブロック引数みたいな感じの関数です。

第1、第2引数で図の領域の幅・高さを指定して、その領域に図式を書き込むための関数をレコードに詰め込んで第3引数の関数に渡し、その結果のgraphicsのリストを（枠線加えて）描画する、という動作になります。 「描画機能を詰め込んだツールボックスを渡すから後は自分で頑張って描いてね」という具合です。(以下の説明ではこの第3引数の関数に渡されるレコードのことを"ツールボックス"と勝手に呼んで行きます。)

もしSATySFi言語の見た目がRuby風だったら↓こんなですかね。

d = CD::diagram(360, 240) {|toolbox|
  a = toolbox.obj(...)
  b = toolbox.obj(...)
　[
   toolbox.draw_obj ... ,
   toolbox.draw_arr ... ,
   ...
  ].flatten
}

draw-objとかdraw-arrとかモジュールから直接使えるようにしないのはナンデ？って話なんですが、

• SATySFiの図形描画系関数が取る位置指定引数って基本的にページ内の絶対座標だけど、図の入る位置からの相対座標で指定したいよね
• 図式内で描画する数式のフォント設定だとかは図の入る場所のテキスト処理文脈の物と揃えたいよね

などの事情があるので、この辺をよしなに解決できるよう基点の座標だとかテキスト処理文脈が設定済みのツールボックスをユーザー指定の関数に引き渡すような仕組みになってる物と思われます。

それではこのツールボックスの中身を見ていきましょう。

obj

型objとツールボックスのフィールドのobj関数とありますが、型objは可換図式の対象(頂点)を表す型です。

  type obj = point * graphics

座標とgraphicsのタプルとなっています。

ツールボックスのフィールドの方は

  obj : point -> math -> obj;

この関数は座標と数式を引数に取り、数式をgraphics化した物と座標をタプルにしてobj型データとして返します。

draw-obj

  draw-obj : obj -> graphics list;

obj型データを引数に取り、graphicsを取り出してlistにして返します。

draw-arr, draw-dashed-arr

  draw-arr        : math -> float -> length -> obj -> obj -> graphics list;
  draw-dashed-arr : math -> float -> length -> obj -> obj -> graphics list;

対象間の射(矢)を書く関数です。draw-arrは実線、draw-dashed-arrは点線の矢印を描きます。 引数の型と内容は共通で、順に以下の通り

1. math : 射に対応する数式
2. float : 矢印の始点を0.0 終点を1.0として、数式をどの辺りに表示するか
3. length : 数式を矢印からどれだけ離して配置するか (正なら進行方向に向かって右、負なら左に配置）
4. obj : 射の始点となる対象
5. obj : 射の終点となる対象

返り値はgraphicsのlistです。

ツールボックスのフィールドは以上の4つです。

\diagramコマンドに引数として渡す関数は、渡されたツールボックスのobj関数で数式をgraphics化し、そしてdraw-objやdraw-arrで得られるgraphicsのlistを結合して返してやればOKなわけです。

2. 実際に描いてみよう

というわけで、まずは簡単な図をベタに書いてみましょう。

@require: stdja
@require: math
@require: cd

let testdiag toolbox =
  let a = toolbox#obj (40pt, 85pt) ${A} in
  let b = toolbox#obj (110pt, 85pt) ${B} in
  let c = toolbox#obj (40pt, 25pt) ${C} in
  let d = toolbox#obj (110pt, 25pt) ${D} in
  let objs = List.map toolbox#draw-obj [a; b; c; d] |> List.concat in
  let f = toolbox#draw-arr ${f} .45 -10pt a b in
  let g = toolbox#draw-arr ${g} .5 5pt a c in
  let h = toolbox#draw-arr ${h} .5 -10pt b d in
  let k = toolbox#draw-arr ${k} .45 10pt c d in
    List.concat [objs; f; g; h; k]

in
document (|
  title = {};
  author = {};
  show-title = false;
  show-toc =false;
|) '<
  +p{ \CD.diagram(150pt)(115pt)(testdiag); }
>

処理結果↓

図1.

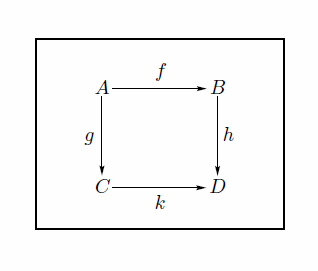
キレイにできましたね。

3. もうちょっと楽に描きたい

obj, draw-obj, draw-arrをいっぱい書かなきゃだったりdraw-objとdraw-arrの返すgraphicsのlistをまとめるのちょっとダルい…ダルくない? という事で、若干書くのが楽になる（かもしれない）ヘルパーコマンドを作ってみました。

let-inline ctx \cdutil width height objects edges =
  let diagf r =
    let sz = get-font-size ctx in
    let objs = List.map (fun (l, m, p) -> (l, r#obj p m)) objects in
    let objg = List.map (fun (_, o) -> r#draw-obj o) objs in
    let obj label =
      match List.assoc string-same label objs with
      | None    -> r#obj (0pt, 0pt) ${}
      | Some(o) -> o
    in
    let arrg = List.map (fun (s, e, m, t, l) ->
        r#draw-arr m t (0pt -' (sz *' l)) (obj s) (obj e)
      ) edges in
    List.append objg arrg |> List.concat
  in
    read-inline ctx {\CD.diagram(width)(height)(diagf);}

引数width heightは\CD.diagramにそのまま渡します。

objectsは対象を表すリストで、obj型データのリストではなく(string * math * point)のリストを指定します。obj型データにラベルとして文字列を加えた型になっています。

edgesは射のリストで、(string * string * math * float * float)のリストです。 内容は左から順に以下の通り

1. string : 射の始点の対象を示すラベル文字列
2. string : 射の終点の対象を示すラベル文字列
3. math : 射に対応する数式 (draw-arrの第1引数)
4. float : 矢印の始点を0.0 終点を1.0として、数式をどの辺りに表示するか (draw-arrの第2引数)
5. float : 数式を矢印からどれだけ離して配置するか (draw-arrの第3引数をフォントサイズに対する倍率指定にした物)

コイツを使うと

  +p{
    \cdutil(305pt)(125pt)
    [(`A`, ${A}, (30pt, 90pt));
     (`B`, ${B}, (90pt, 90pt));
     (`C`, ${C}, (150pt, 90pt));
     (`D`, ${D}, (210pt, 90pt));
     (`E`, ${E}, (270pt, 90pt));
     (`A'`, ${A'}, (30pt, 30pt));
     (`B'`, ${B'}, (90pt, 30pt));
     (`C'`, ${C'}, (150pt, 30pt));
     (`D'`, ${D'}, (210pt, 30pt));
     (`E'`, ${E'}, (270pt, 30pt))
    ]
    [(`A`, `B`, ${f}, 0.4, 1.0);
     (`B`, `C`, ${g}, 0.4, 1.0);
     (`C`, `D`, ${h}, 0.4, 1.0);
     (`D`, `E`, ${j}, 0.4, 1.0);
     (`A`, `A'`, ${l}, 0.4, 1.0);
     (`B`, `B'`, ${m}, 0.4, 1.0);
     (`C`, `C'`, ${n}, 0.4, 1.0);
     (`D`, `D'`, ${p}, 0.4, 1.0);
     (`E`, `E'`, ${q}, 0.4, 1.0);
     (`A'`, `B'`, ${r}, 0.4, 0.-.1.);
     (`B'`, `C'`, ${s}, 0.4, 0.-.1.);
     (`C'`, `D'`, ${t}, 0.4, 0.-.1.);
     (`D'`, `E'`, ${u}, 0.4, 0.-.1.)
    ];
  }

で結果が

図2

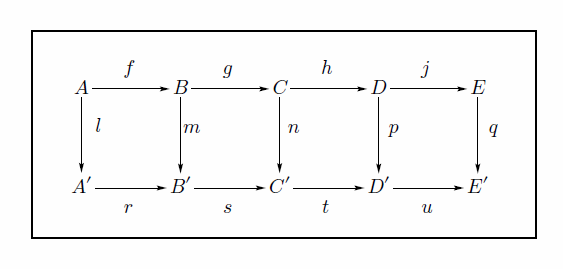
大きめの図式でも書きやすくなってるんじゃないでしょうか。

4. おまけ

objやdraw-arr関数に渡す数式について。 これ、ガワが数式(math型データ)なら何でも良いので、インラインテキストを引数に取る数式コマンド\textを使えば何でも詰め込めちゃうんですよね。

というわけで以下お遊び。

  +p{
    \cdutil(200pt)(90pt)
     [(`A`, ${A}, (180pt, 20pt));
      (`B`, ${B}, (30pt, 20pt))
     ]
     [(`A`, `B`, ${\text!{\insert-image(50pt)(`genbaneko.jpg`);}}, 0.7, 0.-.0.4)];
  }
  +p{
    \cdutil(200pt)(90pt)
     [(`neko`, ${\text!{\insert-image(80pt)(`genbaneko_.jpg`);}}, (150pt, 10pt));
      (`d`, ${}, (120pt, 50pt));
      (`logo`, ${\text!{\SATySFi;}}, (40pt, 50pt))
     ]
     [(`d`, `logo`, ${\text!{ヨシ!}}, 0.7, 0.-.1.)];
  }

ヨシ!

---

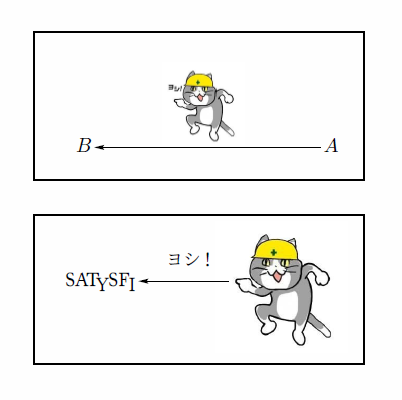
以上cdパッケージの使い方の紹介でした。 今回書いたコードはこのGistにまとめておきましたので参考にしてみてください。

ご安全に！

SATySFiで数式を生成する ～アッカーマン関数編～

これは2018 SATySFi advent calendar 6日目の記事です。[前] [次]

たとえば話の流れでアッカーマン関数の計算方法の説明が必要になったとき(例1)、手打ちで数式を書きたくはないですよね。 何らかの数式処理システムで式を生成して適当な形式でエクスポートするか、スクリプト言語で式を生成するプログラムを書くか検討する所です。

例1. 寿司～虚空編～ (小林銅蟲) 第2話より

この後8ページほど数式が続く

しかし2017年人類は高度なデータ表現能力・アルゴリズム記述能力・数式組版能力を併せ持った組版システム“SATySFi”を手に入れました。 プログラム生成できるようなタイプの数式ならシュッと生成して美しく組み上げてpdf出力まで出来ちゃいますので、今回はコイツで全部やって行きます。

1. 計算式のデータ表現を作る

まずアッカーマン関数の定義ですが、

Wikipediaより

これをSATySFiの関数として書き下すと以下の通り。

let-rec ack
  | n 0 = n + 1
  | 0 m = ack 1 (n - 1)
  | n m = ack (n - 1) (ack n (m - 1))

パターンマッチ構文便利ですね。

ただこれだと普通のint -> int型の関数で、数値を渡して評価すると最終計算結果の数値が返ってくるだけです。 今回は計算過程の式が欲しいので、計算式をデータとして表現し、その計算式データを定義通りに変形していく処理を実装する必要があります。

寿司2話に倣って引き算の所は結果の数値のみ書き出す事にすると、計算式に出てくるのは次の2要素のみ。

• 数値
• 2引数の関数適用 (引数は数値 or 関数の再帰適用)

数値を葉とした単純な二分木で良さそうですねという事で、計算式データの型は以下のように定義。

type aexpr =
  | Num of int
  | Fun of aexpr * aexpr

これでは Fun(Num(3), Num(3)), は Fun(Num(2), Fun(Num(3), Num(2))) のように代数的データ型の値として書けるようになりました。

2. 計算処理の実装

計算式データの計算を1ステップ分進める関数calc1を実装します。

let-rec calc1
  | (Num(n))              = Num(n)
  | (Fun(Num(0), Num(n))) = Num(n + 1)
  | (Fun(Num(m), Num(0))) = Fun(Num(m - 1), Num(1))
  | (Fun(Num(m), Num(n))) = Fun(Num(m - 1), Fun(Num(m), Num(n - 1)))
  | (Fun(x, y))           = Fun(x, calc1 y)

5つのパターンに分けて処理してますが内容は上から順に以下の通り。

1. 数値が渡された時。これ以上計算する物はないのでそのまま返す。
2. という形の式が渡された時。第2引数に1を加えた数値を返す。
3. という形の式が渡された時。式を返す。
4. という形の式が渡された時。式を返す。
5. 上記4つ以外、即ちという形の式が渡された時。第2引数を1ステップ進めた式に置き換えた式を返す。

パターンマッチと再帰呼出しのおかげでスッキリ書けちゃいますね。 念のため正しく計算されてるかを確かめてみましょう。 計算式データを文字列化し、display-messageでコンソールに出力します。

...

let-rec aexpr2str
  | (Num(n))    = (arabic n)
  | (Fun(x, y)) = `A(` ^ (aexpr2str x) ^ `,` ^ (aexpr2str y) ^ `)`

let-inline \test =
  let f e = let () = display-message (aexpr2str e) in calc1 e in
  let _ = Fun(Num(1), Num(1)) |> f |> f |> f |> f |> f |> f in
    {done}

in
document (|
  title = {};
  author = {};
  show-title = false;
  show-toc = false;
|) '<
  +p{\test;}
>

↓コンソール出力

...
 ---- ---- ---- ----
  evaluating texts ...
A(1,1)
A(0,A(1,0))
A(0,A(0,1))
A(0,2)
3
3
  evaluation done.
 ---- ---- ---- ----
...

良さそうですね。あとは渡されたaexpr型データにcalc1を繰り返し適用し、Num(n)に収束するまでの過程を リストに溜め込んで返す関数を作れば計算式生成処理の完成です。

let calc-all e0 =
  let-rec repeat e a =
    match e with
    | Num(_) -> List.reverse (e :: a)
    | _      -> repeat (calc1 e) (e :: a)
  in
    repeat e0 []

3. 計算式データを数式(math型データ)に変換する

日本語が紛らわしくなっちゃってますが、この記事では

• 計算式データ ＝ aexpr型データ
• 数式 ＝ SATySFiの組版用数式データ (math型データ)

です。生成した計算式データを文書として出力するには、文書中に数式として入れ込まなければなりません。

というわけで今回の数式生成の肝である、計算式データを数式に変換する関数を作ります。

let-rec expr2math
  | (Num(n))    = math-char MathOrd (arabic n)
  | (Fun(x, y)) =
    let x = expr2math x in
    let y = expr2math y in
      ${A\( #x, #y \)}

構造は先程テストに使った文字列化関数expr2strとほぼ同じなんですが、こちらはなんやかんやしてmath型データを返すようになっています。

数値の数式化

引数がNum(n)つまり数値の時ですが、int型データnを数式にするにはまず関数arabicで文字列化し、その結果を関数math-charで数式化すればOK。

math-charの第2引数は数式の前後のスペーシングを制御するための“数式クラス”指定で、数値の場合は“通常”を表すMathOrdを使います。

数式クラス指定は他にMathRel, MathBinなど全部で9種類ありますが、詳しく知りたい人はThe SATySFi Bookの10章とLambdaNote社から刊行されている数式組版の2章(図1.)を読むと良いでしょう。

図1. 数式組版 (木枝祐介) 2章より

スペーシングの図解

関数適用式の数式化

引数がFun(x, y)の場合ですが、まず引数のxとyをそれぞれ再帰処理で数式データ化しておき、最後に数式リテラル中に埋め込んで返します。

数式中に'#'+'変数名'と書くことで、よくあるスクリプト言語の文字列補間機能のノリで変数に束縛されている数式データを埋め込むことができます。

簡単ですがこれで肝のaexpr型→math型変換は完了。 calc-allで得られた計算式のリストにList.map aexpr2mathを適用すれば組版readyな数式のリストの出来上がり。

4. 数式を並べる

数式のリストが出来たらあとはもう数式用ブロックコマンド+alignに渡してキレイに並べてもらうだけ、 だったら良かったんですが、残念ながら+alignはページをまたぐことができないので今回はコマンドを自作。

let-block ctx +eqns mlst =
  let em = embed-math ctx in
  let print ib = line-break true true ctx (ib ++ inline-fil) in
  match mlst with
  | []        -> block-nil
  | f::[]     -> print (em f)
  | f::(s::r) ->
    let margin = match space-between-maths ctx f ${=} with
      | None       -> inline-nil
      | Some(ibsp) -> ibsp
    in
    let indent = inline-skip (get-natural-width (em f)) ++ margin in
    let p m = print (indent ++ (em ${= #m})) in
      List.map p r
      |> List.fold-left (+++) (print (em ${#f = #s}))

これはまあページをまたぐようなネタ数式のためだけのその場しのぎコマンドなので説明は略。 普通は+alignコマンドとか使いましょう。

5. 完成

まとめとして、数値2つを渡されたらaexpr型のデータにして2～4の処理を順に適用していく+Ackコマンドを作って完成。

let-block ctx +Ack m n =
  let ms = Fun(Num(m), Num(n))
         |> calc-all
         |> List.map expr2math
  in
    read-block ctx '<+eqns(ms);>

+Ack(3)(1);を出力した結果がこちら。

ソース全体とpdf → SATySFiでアッカーマン関数

自由にパラメータを変えて遊んでみてください、と言いたい所ですが +Ack(3)(4);はフォントサイズ5pt, 段落マージン1ptの設定でA4用紙185ページほどになります。 Ack(3, 5), Ack(4, 0)くらいまでは大丈夫かもしれませんが、それ以上はまず死ぬと思いますのでご注意ください。

have fun!

C言語をコンパイルするSELECT文(SQLite3用)を作った

@shinhさん作のコンパイラインフラストラクチャELVMに SQLite3シェル用のSQLを吐き出すバックエンドを足して@rui314さん作のCコンパイラ8ccを SQLにコンパイルし、29万行のSELECT文から成るCコンパイラが出来上がりました。

https://github.com/youz/8cc-sqlite3

こちらからCコンパイラ&ELVM IRアセンブラが ビューの形で入っているSQLite3のデータベースファイルを入手できます。

使い方

JSON1拡張が有効になっているバージョンのSQLite3シェルを使用します。 SQLite公式サイトで配布しているバイナリやDebianパッケージのsqlite3 ver.3.11 とかでOK。

$ sqlite3 elvm.db3

1. Cソース読み込み

elvm.db3を読み込んだら、テーブルsrc(b BLOB)にコンパイルしたいCプログラムを入れます。

(注意) #includeを含むCソースはコンパイルできません

DELETE FROM src;
INSERT INTO src(b) VALUES('
int putchar(int c);
int main() {
  const char* p = "Hello, world!\n";
  for (; *p; p++)
    putchar(*p);
  return 0;
}');

あるいはreadfile関数を使ってファイルから読み込むと簡単です。

INSERT INTO src(b) VALUES(readfile('sample/hello.c'));

2. C → ELVM IR コンパイル

8ccをSQL化したビューelvm_8ccからstdout列をSELECTし、テーブルeir(b BLOB)に入れます。

DELETE FROM eir;
INSERT INTO eir(b) SELECT stdout FROM elvm_8cc;

(注意) 先のHelloWorldのコンパイルにはCore i5 2.5GHzのマシンで30分ほどかかります

3. ELVM IRのアセンブル

最後にELVM IRをELVMが対応している各種バックエンド言語にアセンブルするわけですが、 出力先言語は設定テーブル option(target TEXT) のtarget列に書き込んで指定します。 (optionテーブルには1行だけレコードが入っています)

UPDATE option SET target = 'rb';

出力先言語とそれに対応する文字列はREADMEに書いてあります。 もしくはDB内のsupported_targetsテーブルを見てください。

アセンブル処理はビュー elvm_elc からSELECT。

SELECT writefile('hello.rb', stdout) FROM elvm_elc;

(注意) HelloWorldのELVM IR→Rubyへのアセンブルには大体20分ほどかかります

Rubyにアセンブルした結果はこんな感じ

$ cat hello.rb
@a = 0
@b = 0
@c = 0
@d = 0
@bp = 0
@sp = 0
@pc = 0
@mem = [0] * (1 << 24)
@mem[0] = 72
@mem[1] = 101
@mem[2] = 108
@mem[3] = 108
@mem[4] = 111
@mem[5] = 44
@mem[6] = 32
@mem[7] = 119
@mem[8] = 111
@mem[9] = 114
@mem[10] = 108
@mem[11] = 100
@mem[12] = 33
@mem[13] = 10
@mem[15] = 16


def func0
 while 0 <= @pc && @pc < 512
  case @pc

  when 0
   true && @pc = 1 - 1

  when 1
   @d = @sp
   @d = (@d + 16777215) & 16777215
   @mem[@d] = @bp
   @sp = @d
   @bp = @sp
   @sp = (@sp - 1) & 16777215
   @a = 0
   @b = @sp
   @a = 0
   @b = @bp
   @b = (@b + 16777215) & 16777215
   @mem[@b] = @a

  when 2
   @b = @bp
   @b = (@b + 16777215) & 16777215
   @a = @mem[@b]
   @b = @a
   @a = @mem[@b]
   @a == 0 && @pc = 4 - 1

  when 3
   true && @pc = 5 - 1

  when 4
   true && @pc = 7 - 1

  when 5
   @b = @bp
   @b = (@b + 16777215) & 16777215
   @a = @mem[@b]
   @b = @a
   @a = @mem[@b]
   @d = @sp
   @d = (@d + 16777215) & 16777215
   @mem[@d] = @a
   @sp = @d
   putc @a
   @sp = (@sp + 1) & 16777215

  when 6
   @b = @bp
   @b = (@b + 16777215) & 16777215
   @a = @mem[@b]
   @d = @sp
   @d = (@d + 16777215) & 16777215
   @mem[@d] = @a
   @sp = @d
   @a = (@a + 1) & 16777215
   @b = @bp
   @b = (@b + 16777215) & 16777215
   @mem[@b] = @a
   @a = @mem[@sp]
   @sp = (@sp + 1) & 16777215
   true && @pc = 2 - 1

  when 7
   @a = 0
   @b = @a
   exit
   exit
  end
  @pc += 1
 end
end

while true
 case @pc / 512
 when 0
  func0
 end
end

$ ruby hello.rb
Hello, world!

コンパイル&アセンブルを1度に済ませたい時はelvm_8cc_elcからSELECTしてください。最初から書くと

DELETE FROM src;
INSERT INTO src(b) VALUES(readfile('source.c'));
UPDATE option SET target = 'js';
SELECT writefile('output.js', stdout) FROM elvm_8cc_elc;

samplesフォルダにELVM本家のテストから3つほど#includeのない(あるいは処理済みの)物を 選んで入れてありますので、暇だったら遊んでみてください。

(注意) sample/fizzbuzz.cのコンパイルはめっちゃ時間かかります(計測放棄)

バックエンドの解説

SQL文中でループ等の制御構文を使えるDBMSならRubyやJS等とほぼ変わらない仕組みで バックエンドが書けそうですが、制御構文もストアドプロシージャもないSQLite3で どうやってやるかっていうと、ver 3.8.3でサポートされたRecursive Common Table Expression(以下再帰CTE)で実現できます。

再帰CTE

再帰CTEっていうのは、知らない人向けに説明すると関数型言語に良くある unfold関数と同じような再帰的展開処理をSELECT文で実現できる仕組みです。

Scheme(SRFI-1)のunfoldの定義は以下の通り

(unfold p f g seed [tail-gen]) =
  (if (p seed)
      (tail-gen seed)
      (cons (f seed)
            (unfold p f g (g seed))))

;; Gaucheでの使用例
(use srfi-1)
(unfold (lambda (e) (> e 10))    ; 終了判定をする関数 p
        (lambda (e) (* e e))     ; seedをリストの要素に変換する関数 f
        (lambda (e) (+ e 1))     ; seedから次のseedを生成する関数 g
        0)                       ; seed
        ; tail-genは省略可。デフォルトは (lambda (x) '())
;-> (0 1 4 9 16 25 36 49 64 81 100)

-- 再帰CTEの例
WITH RECURSIVE
  rec(e) AS (
    SELECT 0                      -- seed
    UNION SELECT e + 1 FROM rec   -- g
    WHERE e < 10                  -- p
  )
SELECT e * e FROM rec;            -- f

0
1
4
9
16
25
36
49
64
81
100

見比べるとコードのコメントにp, f, g, seedと書いてある行がそれぞれ 対応している事が分かるかと思います。

ちなみに再帰CTEでのseedは単一レコードではなくても良いので、再帰する毎に レコード数が変化するような処理も書けます。 (UNION SELECTが返すレコードセットが0件になった時点で再帰が止まる、 という仕組みになっています。)

-- 7回再帰して255レコードを生成する例
WITH
  d(i) AS (SELECT 0 UNION SELECT 1),
  r(i, v) AS (
    SELECT 1, 1
    UNION SELECT r.i + 1, r.v*2 + d.i
    FROM r CROSS JOIN d
    WHERE r.i < 8
  )
SELECT i, v FROM r;

1|1
2|2
2|3
3|4
3|5
3|6
3|7
4|8
4|9
4|10
...
8|253
8|254
8|255

その他のサンプル

• 公式ドキュメントのマンデルブロ集合をプロットするSQLと数独を解くSQL
• Anarchy Golfのチューリングマシーン問題を解く拙作のインタープリタ

ELVMの実装

さてこの再帰CTEでELVMバックエンドをどうやって作るかというと、

• VMの状態(レジスタ、プログラムカウンタ(pc)、メモリ、IO等)を1レコードで表現する
• インストラクション列を状態遷移としてUNION SELECTの部分で表現する

これが出来ればOK。

レジスタ、pc、フラグ等はINT、stdin/stdoutはTEXTとして単純に持てば良いのですが メモリがちょっと面倒。テーブルで表現できれば楽なんですがSELECT文中からテーブルを 更新するような事は出来ないので値として持つ必要があります。

BLOBでメモリを表してみたら書き換え時にメモリ食いまくって一瞬でメモリ不足エラーになってダメだったので、 遅そうだけれども省メモリで着実に動作してくれるJSON1拡張のjson_object形式でメモリを持つことにしました。

状態遷移ですが、1つのpcが指すコードブロック中の命令列に連番(コード中ではstepと表現)を振って、 pcとstepの組で状態を表す事にします。

で、あとはCASE式を機械的に組んでいけばOKなんですが、CASE式が表現できるのは あくまで1つの値なので、VMを表すレコードの各列ごとに状態遷移を書く必要があり、 単純な処理でもコンパイル結果は大分悲惨な事になります。

例えばELVMのテストにある02mov.eirは

mov A, 43    # pc=1 step=0
putc A       # pc=1 step=1
exit         # pc=1 step=2

• (pc, step) = (0, 1)だったらレジスタAに43をセット
• (pc, step) = (0, 2)だったらstdoutにstdout+char(A)をセット
• (pc, step) = (0, 3)だったらrunningに0をセット

という状態遷移になるのですが、SQLへアセンブルした結果がこちら↓

DROP TABLE IF EXISTS stdin;
CREATE TABLE stdin(i BLOB);
INSERT INTO stdin(i) VALUES(readfile('input.txt'));
DROP TABLE IF EXISTS data;
CREATE TABLE data(i INT PRIMARY KEY, v INT);
INSERT INTO data VALUES
  (0,1)
;
-- .stats on
WITH
 elvm AS (
  SELECT
   0 a,
   0 b,
   0 c,
   0 d,
   0 bp,
   0 sp,
   0 pc,
   0 step,
   1 running,
   (SELECT json_group_object(i, v) FROM data) mem,
   (SELECT i FROM stdin) stdin,
   '' stdout,
   0 cycle
  UNION ALL SELECT
   CASE pc / 512
   WHEN 0 THEN
    CASE pc
    WHEN 1 THEN
     CASE step
     WHEN 0 THEN 43
     ELSE a END
    ELSE a END
   ELSE a END
   ,
   b
   ,
   c
   ,
   d
   ,
   bp
   ,
   sp
   ,
   CASE pc / 512
   WHEN 0 THEN
    CASE pc
    WHEN 0 THEN
     CASE step
     WHEN 0 THEN 1
     WHEN 1 THEN pc+1
     ELSE pc END
    WHEN 1 THEN
     CASE step
     WHEN 2 THEN pc+1
     ELSE pc END
    END
   END
   ,
   CASE pc / 512
   WHEN 0 THEN
    CASE pc
    WHEN 0 THEN
     CASE step
     WHEN 0 THEN 0
     WHEN 1 THEN 0
     ELSE step + 1 END
    WHEN 1 THEN
     CASE step
     WHEN 2 THEN 0
     ELSE step+1 END
    END
   END
   ,
   CASE pc / 512
   WHEN 0 THEN
    CASE pc
    WHEN 1 THEN
     CASE step
     WHEN 2 THEN 0
     ELSE running END
    ELSE running END
   ELSE running END
   ,
   mem
   ,
   stdin
   ,
   CASE pc / 512
   WHEN 0 THEN
    CASE pc
    WHEN 1 THEN
     CASE step
     WHEN 1 THEN stdout||char(a)
     ELSE stdout END
    ELSE stdout END
   ELSE stdout END
   ,
   cycle + 1
  FROM elvm WHERE running = 1
 )
SELECT writefile('output.txt', stdout) FROM elvm WHERE running = 0;

恐ろしく見通しが悪いですね！

コンパイラのSQLともなると、JMPするわけでもない連続した処理なのに次は10万行後、 その次はそこから15万行前とか、そういう酷いコードになります。 printfデバッグがしやすいのがせめてもの救い。(最後のSELECT文をいじって stdout以外の列も持ってきたり途中経過を持ってきたりするようにするだけ)

つい先日SQLite3に導入されたRow Valuesが使えたら 大分マシになるのかなと思いますが、残念ながら現時点ではCASE式の値としては使えません。

というわけでちょっとしたコードでも悪夢のようなSQLになってしまいますが、 無事ELVMの全テストをパスするバックエンドが出来上がりました。

おまけ：処理速度について

メモリの書き換えが

1. JSON形式の文字列データをパースする
2. 指定されたキーの値を書き換える
3. データをJSON形式で文字列化する

という処理になっている(JSON1拡張はDBにJSON型を導入するのではなく、 文字列型データをJSONとしてパースした上で色々する機能を導入する拡張)ので、 メモリアクセスがボトルネックになってるだろうなと。 (そもそもテーブルでなく値で持ってるので、書き換えの度にコピーする前提)

という訳で実験として、単純で邪悪なSQLite3拡張を作ってみました。

garray.c

gainitでメモリ上に1つ配列を作り、garefで参照、gasetで書き換えます。 評価順が一意に決まるような所でしか使えない、DBMSには入れるべきでないアレな代物です。

JSONの代わりにこの配列拡張を使ってみた結果、30分かかっていたHelloWorldの コンパイル時間が2分ちょうど位になりました。

ドメイン特化言語で2分なら割と良い性能なのではないでしょうか(要出典)