SATySFiで数式を生成する ~ラムダ計算編~
これは2018 SATySFi advent calendar 13日目の記事です。[前] [次]
たとえば何かの資料を書いてる中でラムダ計算の説明が必要になった時、ちょっと込み入ったサンプルを手で書こうとしたら大変です。
PRED 5 = (λnfx.n (λgh.h(gf)) (λu.x) (λu.u)) (λfx.f(f(f(f(fx))))) → λfx.(λf'x'.f'(f'(f'(f'(f'x'))))) (λgh.h(gf)) (λu.x) (λu.u) → λfx.(λgh.h(gf)) ((λgh.h(gf)) ((λgh.h(gf)) ((λgh.h(gf)) ((λgh.h(gf)) (λu.x))))) (λu.u) → ▂▅▇█▓▒░(‘ω’)░▒▓█▇▅▂
心を無にして手を動かせばどうとでもなるんでしょうが誤植が怖い。
そこでSATySFiを使えば計算から組版まで全自動で出来ちゃうんじゃないかな? という事で、ラムダ計算の計算式の生成方法を考えて行きます。
1. データ表現と計算処理の実装
考えて行きますと言ったばかりですが、計算方法についてこれはもうとても素晴らしい講義資料を東北大の住井先生が公開して下さってますので、まずそちらをご覧ください。
OCamlによるラムダ計算インタプリタのシンプルな実装が載っていて、ほぼそのままSATySFiに移植できちゃいます。 が、後の組版処理の都合でちょっと改変を加えます。
データ表現とgensym関数
β簡約時の変数名衝突を避けるために一意な名前の変数を生成するgensym関数ですが、資料のコードでは変数名が'g'+連番となっています。
まあg+添字で出力しても良いのですが、せっかくなのでアルファベット+0個以上のプライムで出力するようにしてみましょう、という事でまずラムダ式のデータ型expを以下のように改変。
type exp = | Var of string * int | Abs of exp * exp | App of exp * exp
Var(変数)はただのstringから(string * int)に変更。stringは変数名、intはプライムの数を表します。
それとAbs(λ抽象)のタプルの1要素目(パラメータ変数名)をstringからexp(実際はVarしか入らない)に変更しています。
gensym関数はカウンタを使う所は変わりませんが、カウンタ値を26で割った余りを文字種(a-z)、商をプライムの数とします。また、ユーザー入力の変数名と被らないようにする処理を加えます。
% 変数名比較関数
let vareq x y =
match (x, y) with
| (Var(s, i), Var(t, j)) -> string-same s t && i == j
| _ -> false
% 汎用リスト検索関数
let-rec find eq x l =
match l with
| [] -> None
| e :: r -> if eq x e then Some(e) else find eq x r
% gensym用カウンタ
let-mutable sym-counter <- -1
% ユーザー入力式中の全変数を入れておくリスト
let-mutable sym-used <- []
% 変数生成関数
let-rec gensym () =
let () = sym-counter <- !sym-counter + 1 in
let c = string-unexplode [!sym-counter mod 26 + 97] in
let p = !sym-counter / 26 in
let v = Var(c, p) in
match find vareq v !sym-used with
| None -> v
| Some _ -> gensym ()
sym-usedには計算開始前にユーザー入力の式の中の全変数が突っ込まれると思ってください。
計算処理
1ステップ分計算を進めるstep関数ですが、資料の実装ではβ簡約できる箇所が複数あった場合それぞれ計算して結果全部をlistにして返すようになっていて、それはそのままでも良いのですが今回は最終的に1通りの簡約方法でしか出力しないので1つの結果をoptionで返す(簡約できなかったらNoneを返す)ように変更します。
let-rec step e =
match e with
| Var(x) -> None
| Abs(x, e0) -> (
match step e0 with
| None -> None
| Some(e) -> Some(Abs(x, e))
)
| App(e1, e2) -> (
match e1 with
| Abs(x, e0) -> Some(subst e2 x e0)
| _ -> (
match step e1 with
| Some(e) -> Some(App(e, e2))
| None -> (
match step e2 with
| Some(e) -> Some(App(e1, e))
| None -> None
)))
簡約できなくなるまで計算を進めるrepeat関数は、途中経過の式をlistに溜め込むよう改変し、ついでにreduct-allと名前を変えます。また、簡約が停止しないタイプの式を与えられた時に死なないよう簡約回数のリミッタを指定できるようにしました。
let reduct-all e lim =
let-rec r e a i =
if i > lim then
List.reverse (e :: a)
else
match step e with
| None -> List.reverse (e :: a)
| Some(f) -> r f (e :: a) (i + 1)
in
r e [] 0
ここまでをざっくりテスト。
exp型データを文字列化する関数exp2strを用意し、(λf.λx.f(fx))(λf.λx.f(fx))を計算させてコンソールに出力してみます。
% 必要ない括弧が沢山付くけどキニシナイ
let-rec exp2str
| (Var(x, i)) = x ^ (if i > 0 then (arabic i) else ` `)
| (Abs(x, e)) = `(\` ^ (exp2str x) ^ `.` ^ (exp2str e) ^ `)`
| (App(x, y)) = `(` ^ (exp2str x) ^ (exp2str y) ^ `)`
let-inline \test =
let f = Var(`f`, 0) in
let x = Var(`x`, 0) in
let f2x = Abs(f, Abs(x, App(f, App(f, x)))) in
let () = sym-used <- [f; x] in
let () = reduct-all (App(f2x, f2x)) 100
|> List.iter (fun e -> display-message (exp2str e))
in
{done}
コンソール出力結果
... ---- ---- ---- ---- evaluating texts ... ((\f.(\x.(f(fx))))(\f.(\x.(f(fx))))) (\a.((\f.(\x.(f(fx))))((\f.(\x.(f(fx))))a))) (\a.(\b.(((\f.(\x.(f(fx))))a)(((\f.(\x.(f(fx))))a)b)))) (\a.(\b.((\c.(a(ac)))(((\f.(\x.(f(fx))))a)b)))) (\a.(\b.(a(a(((\f.(\x.(f(fx))))a)b))))) (\a.(\b.(a(a((\d.(a(ad)))b))))) (\a.(\b.(a(a(a(ab)))))) evaluation done. ---- ---- ---- ---- ...
良さそうな感じですね。
2. 数式化
さて本題。exp型データを数式化します。
まず変数Varの文字列化ですが、数式モードで書くようなx''と言った文字列を何も考えずにmath-charに渡すと
let-math \testvar = math-char MathOrd `x''`
...
+p{${ \testvar }}
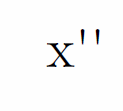
xは直立になるし、プライムを付けるつもりがシングルクォートになってしまっています。math-charは渡された文字列の数式構造を解析したりしないので、xを変数名として認識してイタリックにしたり、シングルクォートをプライムに置き換えたりみたいな事はしないんですね。
ではどうしたら良いかと言うと、文字列を渡すと斜体の数式にして返す\mathit-tokenというコマンドがありまして、変数名部分はコイツを使えばOK。
そしてプライムについては、シングルクォートを置き換えてくれないなら最初からプライム(U+2032)を書いちゃいます。
では実際にexp型のVarデータを数式化してみましょう。
let-rec repeat-string
| s 0 = ` `
| s n = s ^ (repeat-string s (n - 1))
let-math \testvar2 e =
match e with
| Var(s, n) ->
let primes = math-char MathOrd (repeat-string `´` n) in
math-concat ${\mathit-token!(s)} primes
| _ -> ${}
...
+p{${ \testvar2!(Var(`x`, 2)) }}
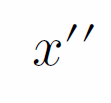
イイ感じになりましたね。そして変数の数式化が出来ちゃえば後はそんなに難しくありません。というわけでドーン
let-rec exp2math
| (Var(x, i)) =
let p = math-char MathOrd (repeat-string `′` i) in
${\mathit-token!(x)#p}
| (Abs(x, e)) =
let mx = exp2math x in
let me = exp2math e in
${\lambda #mx . #me}
| (App(x, y)) =
let mx = exp2math x in
let px = match x with
| Var _ -> mx
| App(_, Var _) -> mx
| _ -> ${\(#mx\)}
in
let my = exp2math y in
let py = match y with
| Var _ -> my
| _ -> ${\(#my\)}
in
math-concat px py
Absはアッカーマン関数の時のFunと同じ要領で、パラメータ(x)と式(e)をそれぞれ数式化しておいてリテラルへ埋め込んじゃえばOk。
Appは括弧が必要な場合と不要な場合の判定でちょっと長くなっちゃってますが、Absと同じようにxとyを再帰処理で数式化した上で、必要な箇所に括弧を貼り付けて横に並べるだけ。
試しに\f'.\x'.f'(f'x')を数式化してみましょう
let-math \testexpr =
let f = Var(`f`, 1) in
let x = Var(`x`, 1) in
exp2math (Abs(f, Abs(x, App(f, App(f, x)))))
...
+p{ ${ \textexpr } }
結果
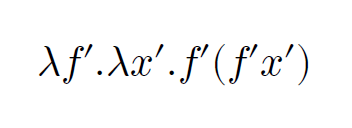
上手に出来ました。(実は問題が潜んでますがそこは追記で説明)
3. 数式を並べる
必要な機能がほぼ揃ったので、仕上げとしてブロックコマンド+lambdacalcを作成します。
gensymで使うカウンタと使用済み変数リストを初期化してから、渡された式を計算→数式化→縦に並べて完成。
今回はページをまたぐような長さの計算をするつもりはないので、数式を並べるのはmathパッケージの+alignコマンドに丸投げです。
let-block ctx +lambdacalc lm lexp =
let () = sym-counter <- -1 in % gensym用カウンターリセット
let () = sym-used <- (dedup vareq (allvar lexp)) in % gensymでの名称被り回避用
let (f::r) = reduct-all lexp 100
|> List.map exp2math in
let ml = [lm; ${= #f}] :: (List.map (fun m -> [${}; ${\to #m}]) r) in
read-block ctx '<+align(ml);>
こんな風に使います。
...
% ラムダ式を簡単に書くためのエイリアス
let var s = Var(s, 0)
let abs v e = Abs(v, e)
let app e1 e2 = App(e1, e2)
% チャーチ数生成
let cnum n =
let f = var `f` in
let x = var `x` in
let-rec r
| 0 a = a
| i a = r (i - 1) (app f a)
in
abs f (abs x (r n x))
in
document (| title = {}; author = {}; show-title = false; show-toc = false; |) '<
+lambdacalc(${3^2})(app (cnum 2) (cnum 3));
>
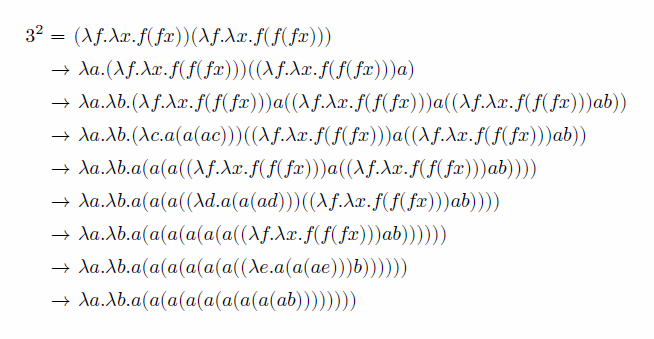
これでメンドクサイ引き算も安心
...
% pred = λn.λf.λx.n (λg.λh.h (g f)) (λu.x) (λu.u)
let pred =
let f = var `f` in
let g = var `g` in
let h = var `h` in
let n = var `n` in
let u = var `u` in
let x = var `x` in
abs n (abs f (abs x (app (app (app n (abs g (abs h (app h (app g f))))) (abs u x)) (abs u u))))
in
document (| title = {}; author = {}; show-title = false; show-toc = false; |) '<
+lambdacalc(${\text!({pred})\ 3})(app pred (cnum 3));
>

以上ラムダ計算をSATySFiに自動で計算&組版させる方法でした。
ソース全体はこちらのGistに。
色々計算させて遊んでみてください。
追記
実はプライムの付け方がこれでは不正解っぽいのです。
 上が
上がexp2mathで生成した数式、下が手打ちの数式\lambda f'. \lambda x'.f'\(f'x'\) をデバッグモードで出力した結果です。プライムは上付きにしないといけないんですね。
math-supという関数で上付きにできるようなので
let-rec exp2math
| (Var(x, i)) =
let p = math-char MathOrd (repeat-string `′` i) in
math-sup ${\mathit-token!(x)} p
...
としてみましたが、そうすると
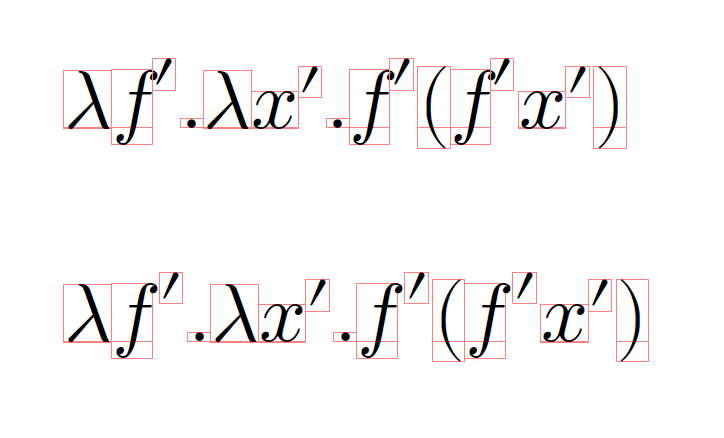
ちょっと調べてもこのスペースの正しい取り方が分からなかったので、これは今後の課題と言うことで。